4 Automatic Matching of Cartridge Case Impressions
Abstract
Forensic examinations attempt to solve the binary classification problem of whether two pieces of evidence originated from the same source.
For example, a cartridge case found at a crime scene may be compared to a cartridge case fired from a suspect’s firearm.
Forensic examiners traditionally rely on high-powered comparison microscopes, case facts, and their own experience to arrive at a source conclusion.
Automatic comparison algorithms have grown in prevalence in a number of forensic
disciplines following the reports from National Research Council (2009) and President’s Council of Advisors on Sci. & Tech. (2016).
Many of these algorithms objectively measure the similarity between evidence, such as two fired cartridge cases, based on markings left on their surface, such as impressions left by a firearm’s breech face during the firing process.
We introduce the Automatic Cartridge Evidence Scoring (ACES) algorithm to compare pairs of three-dimensional topographical surface scans of breech face impressions.
The ACES algorithm pre-processes the scans, extracts numeric features, and returns a similarity score indicating whether two cartridge cases were fired from the same firearm.
The numeric features are computed based on a cell-by-cell registration procedure, results from a density-based unsupervised clustering algorithm, and derived from visual diagnostic tools we developed to investigate the performance of cartridge case comparison algorithms.
We use scans taken at the Roy J Carver High Resolution Microscopy Facility of cartridge cases collected by Baldwin et al. (2014) to train and test the ACES algorithm.
The performance of ACES compares favorably to several other methods, such as logistic regressions on smaller feature sets, random forests, and some variants of previous Congruent Matching Cells methods (Song 2013; Zhang et al. 2021).
We implement the ACES algorithm’s scoring functionality in a free, open-source R package called scored.
4.1 Introduction
A cartride case is the part of firearm ammunition that houses the projectile and propulsive device. When a firearm is discharged and the projectile travels down the barrel, the cartridge case moves in the opposite direction and slams against the back wall, the breech face, of the firearm. Markings on the breech face are “stamped” into the surface of the cartridge case leaving so-called breech face impressions.
In a traditional examination, forensic examiners use these impressions analogous to a fingerprint to determine whether two cartridge cases were fired from the same firearm. The top of Figure 4.1 illustrates this procedure (Xiao Hui Tai 2018; X. Zheng et al. 2014; Vorburger, Song, and Petraco 2015). First, two cartridge cases are collected - perhaps one is from a crime scene and the other is collected from a suspect’s gun. An examiner places the two cartridge cases beneath a “comparison microscope” that merges the views of two compound microscopes into a single split view, similar to the side-by-side cartridge case image in Figure 4.1. The examiner assesses the degree of similarity between the markings on the cartridge cases and chooses one of four conclusions AFTE Criteria for Identification Committee (1992):
Identification: cartridge cases were fired from the same firearm
Elimination: cartridge cases were not fired from the same firearm
Inconclusive: the evidence is insufficient to make an identification or elimination
Unsuitable: the evidence is unsuitable for examination
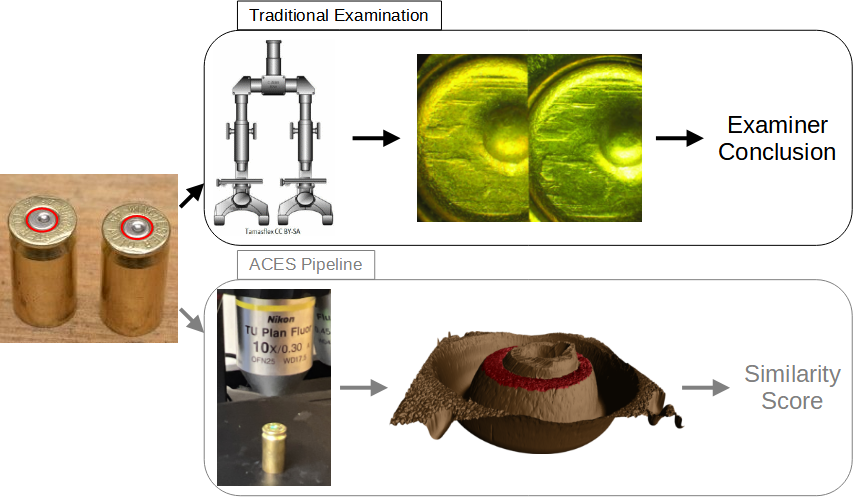
Figure 4.1: Comparison of the traditional examination vs. the currently proposed method for comparing cartridge cases. Both start with two fired cartridge cases. In traditional examination, an examiner uses a microscope to assess the “agreement” of markings on the two cartridge case surfaces. They decide whether or not the cartridge cases were fired from the same firearm, or if there is inconclusive evidence to decide. In the ACES algorithm, we take a topographical scan of the cartridge case surfaces and manually identify the regions containing distinguishable markings (shown in red). We pass these scans to the ACES algorithm, which processes and compares the two scans. The final result is a numerical measure of similarity of the two cartridge cases.
Critics of traditional forensic examinations cite a lack of “foundational validity” underlying the procedures used by firearm and toolmark examiners (National Research Council 2009; President’s Council of Advisors on Sci. & Tech. 2016). In particular, examiners rely largely on their subjective findings rather than on a well-defined procedure to measure similarity. President’s Council of Advisors on Sci. & Tech. (2016) pushed for “developing and testing image-analysis algorithms” to objectively measure the similarity between cartridge cases. An automatic comparison algorithm could supplement, inform, or dictate an examiner’s conclusion (Swofford and Champod 2021).
We introduce a novel Automatic Cartridge Evidence Scoring (ACES) algorithm to objectively compare cartridge case evidence based on their breech face impressions. Our algorithm encompasses all stages of the comparison procedure after collecting a scan of the cartridge case surface including pre-processing, comparing, and scoring. Our ACES algorithm is available open-source as part of the scored R package.
In the following sections, we first review recently proposed algorithms to compare firearm evidence. We then discuss the data collection procedure to obtain 510 cartridge scans used in training and validating the ACES algorithm. To our knowledge, this is the largest published study of a cartridge case comparison algorithm to-date, with the next largest analyzing four different data sets totaling 195 cartridge cases (Chen et al. 2017). After describing the ACES algorithm, we present summary results from training and testing three binary classifier models: base on a random forest, logistic regression, and classification tree. We discuss the strengths and weaknesses of the three classifier models and compare the relative importance of the ACES features. We also argue that the ACES algorithm combines the classification rules of previously proposed cartridge case comparison algorithms while incorporating additional nuance. We conclude with our thoughts on how cartridge case comparison algorithms should be developed, validated, and shared going forward.
4.1.1 Previous Work
Recent proposals for automatic cartridge case scoring algorithms borrow from image processing and computer vision techniques. For example, Vorburger et al. (2007) proposed using the cross-correlation function (CCF) to compare images or scans of cartridge case surfaces. The CCF measures the similarity between two matrices for all possible translations of one matrix against the other. Calculating the CCF while rotating one of the scans therefore allows for estimation of the optimal translation and rotation, together referred to as the registration, between the two scans; simply choose the rotation/translation at which the CCF is maximized. Hare, Hofmann, and Carriquiry (2017) used the CCF, among other features, to compare scans of bullets. Tai and Eddy (2018) developed an open-source cartridge case comparison pipeline that compared cartridge case images using the CCF.
Song (2013) noted that two matching cartridge cases often share similar impressions in specific regions, so calculating the CCF between two full scans may not highlight their similarities. Instead, Song (2013) proposed partitioning one cartridge case scan into a grid of “cells” and calculating the CCF between each cell and the other scan. If two cartridge cases are truly matching, then the maximum CCF value between each cell and the other scan, particularly the cells containing distinguishable breech face impressions, should be relatively large. Furthermore, the cells should “agree” on the registration at which the CCF is maximized. Song (2013) outlined the “Congruent Matching Cells” algorithm to determine the number of cells that agree on a particular registration. A cell is classified as a Congruent Matching Cell (CMC) if its estimated registration is within some threshold of the median registration across all cells and its CCF value is above some threshold. A number of follow-up papers proposed alterations to the the original CMC method (Tong, Song, and Chu 2015; Chen et al. 2017). Joe Zemmels, Hofmann, and VanderPlas (2022) introduced an open-source implementation of the CMC method in the cmcR R package. As an alternative to defining Congruent Matching Cells, Zhang et al. (2021) proposed using a clustering algorithm from Ester et al. (1996) to determine the number of cells in agreement on a specific registration.
Currently, none of these papers have proposed rigorous procedure for comparing different cartridge case comparison algorithms. This includes selecting optimal parameters for a specific algorithm. Joseph Zemmels, VanderPlas, and Hofmann (2023) proposed an optimization criterion to select parameters for the CMC algorithm. Analogously, Hare, Hofmann, and Carriquiry (2017) developed a validation procedure to select parameters for a bullet comparison algorithm. In this work, we introduce a novel cross-validation procedure to learn and test optimal parameters for the ACES algorithm.
4.2 Cartridge Case Data
We use 510 cartridge cases collected as part of a study by Baldwin et al. (2014). The authors of the original study fired 800 Remington 9mm pistol cartridge cases from each of 25 new Ruger SR9, 9mm Luger centerfire pistols.. They separated the collected cartridge cases into 15 sets of four to be sent to each of 218 forensic examiner participants. Each set of four consisted of three cartridge cases labeled as originating from the same firearm, the “known-match” cartridge cases. Participants performed an examination to determine whether a fourth “questioned” cartridge case shared a common source with the known-match triplet (or whether the evidence was inconclusive).
Across all 218 examiners, the true positive rate - proportion of correctly classified matching sets - was reported to be 99.6%. The reported true negative rate - the proportion of correctly classified non-matching sets - was 65.2% The discrepancy between the true positive and true negative rates can be partially explained by the number of “inconclusive” decisions made by the examiners. Examiners reach an inconclusive decision when there is some agreement or disagreement in the characteristics between two cartridge cases, but not enough to make a match or non-match conclusion (AFTE Criteria for Identification Committee 1992). Roughly one out of five comparisons, 22.9%, were reported as inconclusive. The vast majority, 98.5%, of these inconclusives were truly non-matching comparisons, which justifies the true negative rate of 65.2%. There has recently been some debate about how to incorporate inconclusive decisions into accuracy/error rate estimation (Hofmann, Carriquiry, and Vanderplas 2021), so we do not report an overall accuracy here.
We scanned the 510 cartridge cases using the Cadre\(^{\text{TM}}\) 3D-TopMatch High Capacity Scanner.
Briefly, this scanner collects images under various lighting conditions of a gel pad into which the base of a cartridge case is impressed.
Proprietary software that accompanies this scanner combines these images into a 2D array called a surface matrix.
The elements of a surface matrix represent the relative height values of the associated cartridge case surface.
This surface matrix, along with metadata concerning parameters under which the scan was taken (dimension, resolution, author, etc.), are stored in the ISO standard XML 3D Surface Profile (x3p) file type (“Geometrical product specifications (GPS) — Surface texture: Areal — Part 72: XML file format x3p” 2017).
These x3p files can be found at https://github.com/heike/DFSC-scans.
As discussed in the next section, our design differs from that used in Baldwin et al. (2014). Rather than basing error rates on the comparison of three known-match cartridge cases to one questioned cartridge case (3 to 1), we consider the classification error rate of pairwise comparisons (1 to 1). Further, we split the 510 cartridge cases by randomly selecting 10 of the 25 firearms for training and use the remaining 15 firearms for testing. This resulted in a training set of 210 cartridge cases, \(\binom{210}{2} = 21,945\) pairwise comparisons, and a testing set of 300 cartridge cases, \(\binom{300}{2} = 44,850\) pairwise comparisons. We note that there is a large class imbalance between the matching and non-matching comparisons in these data sets (90% of train and 93% of test comparisons are truly non-matching). We discuss how we address this class imbalance in the methods section.
4.3 Methods
We now discuss the methods behind the Automatic Cartridge Evidence Scoring (ACES) algorithm. We divide the methods into three stages:
Pre-processing: prepare cartridge case scans for comparison
Comparing: compare two cartridge cases and compute similarity features
Scoring: measure the similarity between the two cartridge cases using a trained classifier
The following sections detail each of these stages. Throughout, we treat “surface matrix” and “scan” synonymously.
The bottom of Figure 4.1 shows a summary of our procedure. After taking a topographical scan of the cartridge case surfaces, we manually annotate the breech face impression region (shown in red). ACES automatically pre-processes and compares the scans resulting in a similarity score, either a binary classification or class probability, derived from a classifier model.
4.3.1 Pre-processing
We first use the open-source FiX3P web application (https://github.com/talenfisher/fix3p) to manually annotate the breech face impression region. An example of a manually-annotated cartridge case scan is shown in Figure 4.1. The FiX3P software includes functionality to “paint” the surface of a cartridge case using a computer cursor and save the painted regions to a mask. A mask is a 2D array of hexidecimal color values of the same dimension as its associated surface matrix. When initialized, every element of a mask is a shade of brown (#cd7f32) by default. Any elements painted over by the user will be replaced with the user’s selected color value. In Figure 4.1, the breech face impression region was manually annotated using a shade of red (#ff0000).
We pre-process the raw scans by applying a sequence of functions available in the R packages x3ptools (Hofmann et al. 2020) and cmcR (Joe Zemmels, Hofmann, and VanderPlas 2022).
Figure 4.2 shows the effect that each function has on the scan surface values.
Gray pixels in each plot represent missing values in the surface matrix.
The x3p_delete function removes values in the scan based on the associated mask.
Next, the preProcess_removeTrend function subtracts a fitted conditional median plane from the surface values to “level-out” any global tilt in the scan.
The preProcess_gaussFilter() function applies a bandpass Gaussian filter to remove small-scale noise and other large-scale structure, which better highlights the medium-scale breech face impressions.
Finally, the preProcess_erode() function applies the morphological operation of erosion on the edge of the non-missing surface values (Haralick, Sternberg, and Zhuang 1987).
This has the effect of shaving off values on the interior and exterior edge of the surface, which are often extreme “roll-off” values that unduly affect the comparing stage if not removed.
The final result is a cartridge case surface matrix with emphasized breech face impressions.
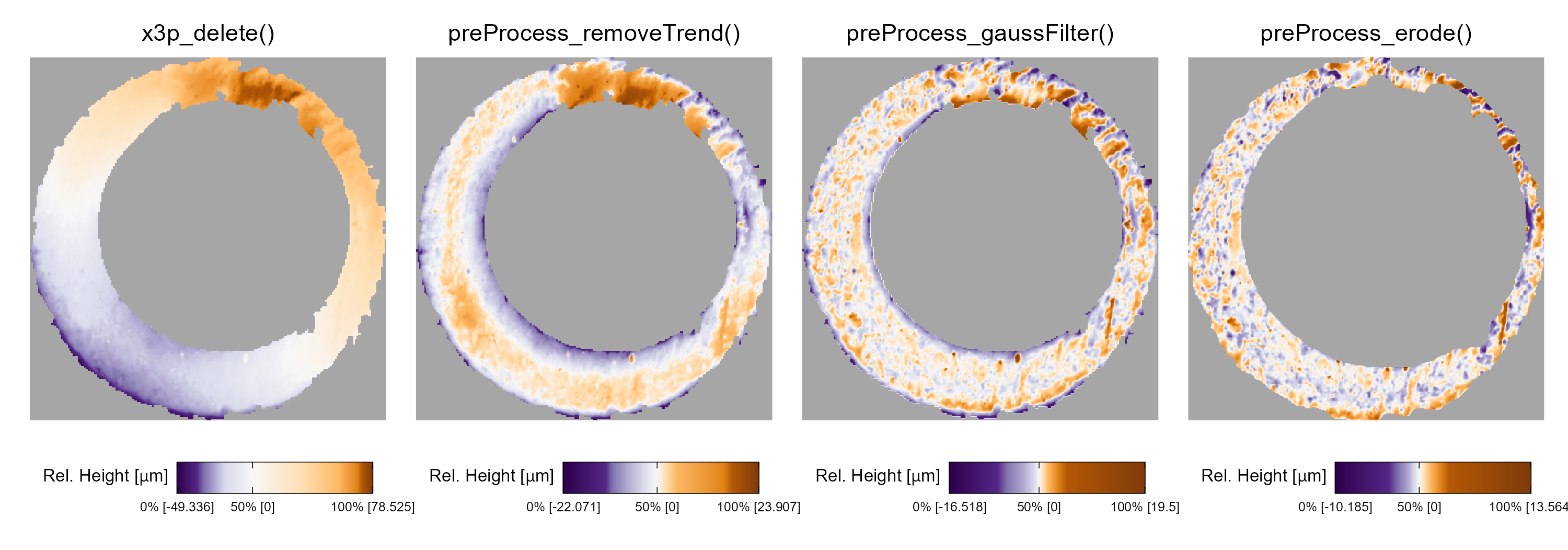
Figure 4.2: We apply a sequence of pre-processing functions to each scan. Each pre-processing step further emphasizes the breech face impressions in the scan.
Next, we compute a set of similarity features for two pre-processed cartridge case scans.
4.3.2 Comparing
In this section, we introduce a set of similarity features for two cartridge case scans. We calculate features at two scales: between two full scans and between individual cells. Analogous to how a forensic examiner uses a comparison microscope with different magnification levels, this allows us to assess the similarity between two scans at the macro and micro levels.
4.3.2.1 Notational Conventions
First, we introduce notation that will be used to define the features. Let \(A\) and \(B\) denote two surfaces matrices that we wish to compare. For simplicity, we assume that \(A,B \in \mathbb{R}^{k \times k}\) for \(k > 0\). We use lowercase letters and subscripts to denote a particular value of a matrix: \(a_{ij}\) is the value in the \(i\)-th row and \(j\)-th column, starting from the top-left corner, of matrix \(A\). We refer to the two known-match cartridge cases in Figure 4.3 as exemplar matrices \(A\) and \(B\).
To accommodate structurally missing values, we adapt standard matrix algebra by encoding the notion of “missingness” into the space of real values as follows: if an element of either matrix \(A\) or \(B\) is missing, then any element-wise operation including this element is also missing.
Standard matrix algebra holds for non-missing elements.
For example, the addition operator is defined as:
\[\begin{align*}
A \oplus_{NA} B = (a_{ij} \oplus_{NA} b_{ij})_{1 \leq i,j \leq k} =
\begin{cases}
a_{ij} + b_{ij} & \text{if both $a_{ij}$ and $b_{ij}$ are numbers} \\
NA &\text{otherwise}
\end{cases}
\end{align*}\]
Other element-wise operations such as \(\ominus_{NA}\) are defined similarly.
For readability, we will use standard operator notation \(+, -, >, <, I(\cdot), ...\) and assume the extended, element-wise operations as defined above.
Note that this definition of dealing with missing values is consistent with a setting of na.rm = FALSE in terms of calculations in R (R Core Team 2017).
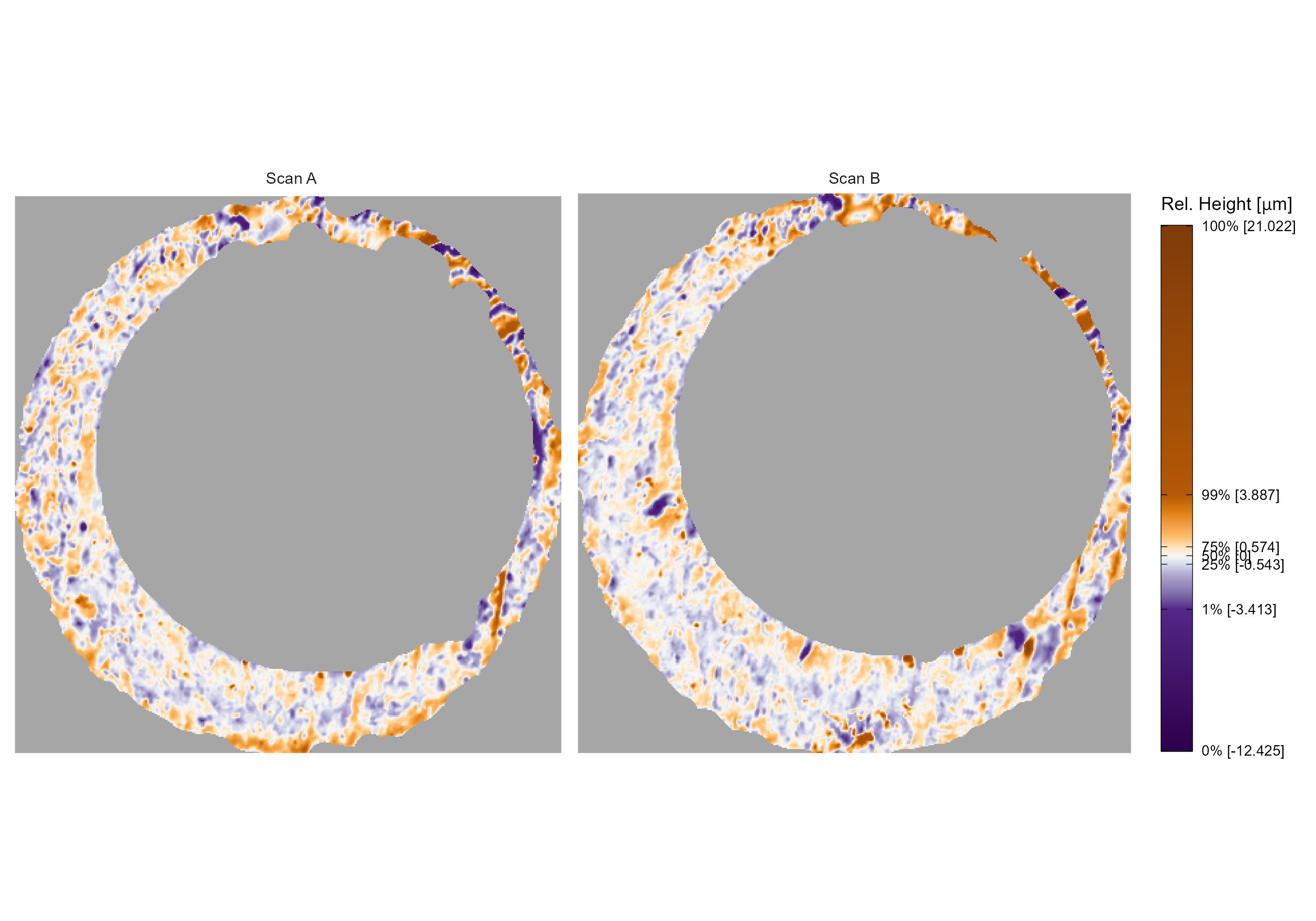
Figure 4.3: A matching pair of processed cartridge case scans. We measure the similarity between these cartridge cases using the distinguishable breech face impressions on their surfaces.
4.3.2.2 Registration Estimation
A critical step in comparing \(A\) and \(B\) is to find a transformation of \(B\) such that it aligns best to \(A\) (or vice versa). In image processing, this is called image registration. Noting that \(A\) and \(B\) are essentially grayscale images with structurally missing values, we rely on a standard image registration technique (Brown 1992).
In our application, a registration is composed of a discrete translation by \((m,n) \in \mathbb{Z}^2\) and rotation by \(\theta \in [-180^\circ,180^\circ]\). To determine the optimal registration, we calculate the cross-correlation function (CCF) between \(A\) and \(B\), which measures the similarity between \(A\) and \(B\) for every possible translation of \(B\), denoted \((A \star B)\). We estimate the registration by calculating the maximum CCF value across a range of rotations of matrix \(B\). Let \(B_\theta\) denote \(B\) rotated by an angle \(\theta \in [-180^\circ,180^\circ]\) and \(b_{\theta_{mn}}\) the \(m,n\)-th element of \(B_\theta\). Then the estimated registration \((m^*,n^*,\theta^*)\) is:
\[ (m^*,n^*,\theta^*) = \arg \max_{m,n,\theta} (a \star b_\theta)_{mn}. \]
In practice we consider a discrete grid of rotations \(\pmb{\Theta} \subset [-180^\circ,180^\circ]\). The registration procedure is outlined in Image Registration Algorithm. We refer to the matrix that is rotated as the “target.” The result is the estimated registration of the target matrix to the “source” matrix.
Image Registration Algorithm
To accommodate missing values, we also compute the pairwise-complete correlation using only the complete value pairs, meaning neither value is missing, between \(A\) and \(B\).
4.3.2.3 Registration-Based Features
4.3.2.3.1 Full-Scan Registration
We first estimate the registration between two full scans \(A\) and \(B\) using Image Registration Algorithm with a rotation grid \(\pmb{\Theta} = \{-30^\circ, -27^\circ,...,27^\circ,30^\circ\}\). This results in an estimated registration \((m^*,n^*,\theta^*)\) and similarity measure \(CCF_{\max}\). We also perform Image Registration Algorithm with the roles of \(A\) and \(B\) reversed, meaning the target scan \(A\) is aligned to source scan \(B\).
To accommodate these two comparison directions, we introduce a new subscript \(d = A,B\), referring to the source scan in Image Registration Algorithm. Consequently, we obtain two sets of sets of estimated registrations, \((m^*_d,n^*_d,\theta^*_d)\) and \(CCF_{\max,d}\), for \(d=A,B\). For \(d = A\), we then apply the registration transformation \((m^*_A,n^*_A,\theta^*_A)\) to \(B\) to obtain \(B^*\) and compute the pairwise-complete correlation, \(cor_{\text{full},A}\), between \(A\) and \(B^*\). We repeat this in the other comparison direction to obtain \(cor_{\text{full},B}\) and average the two:
\[ cor_{\text{full}} = \frac{1}{2}\left(cor_{A,\text{full}} + cor_{B,\text{full}}\right). \]
We assume that the full-scan pairwise-complete correlation is large for truly matching cartridge cases.
4.3.2.3.2 Cell-Based Registration
We next perform a cell-based comparison procedure, which begins with selecting one of the matrices, say \(A\), as the “source” matrix that is partitioned into a grid of cells. The left side of Figure 4.4 shows an example of such a cell grid overlaid on a scan. Each of these source cells will be compared to the “target” matrix, in this case \(B^*\). Because \(A\) and \(B^*\) are already partially aligned from the full-scan registration procedure, we compare each source cell to \(B^*\) using a new rotation grid of \(\pmb{\Theta}'_A = \{\theta^*_A - 2^\circ, \theta^*_A - 1^\circ,\theta^*_A,\theta^*_A + 1^\circ,\theta^*_A + 2^\circ\}\).
We now extend the surface matrix notation introduced previously to accommodate cells. Let \(A_{t}\) denote the \(t\)-th cell of matrix \(A\), \(t = 1,...,T_A\) where \(T_A\) is the total number of cells containing non-missing values in scan \(A\) (e.g., \(T_A = 43\) in Figure 4.4) and let \((a_t)_{ij}\) denote the \(i,j\)-th element of \(A_t\).
The cell-based comparison procedure is outlined in Cell-Based Comparison Algorithm.
Cell-Based Comparison Algorithm
Rather than exclusively returning the registration that maximizes the overall CCF as in Image Registration Algorithm, Cell-Based Comparison Algorithm returns the set \(\pmb{F}_A\) of translations and CCF values for each of the \(T_A\) cells and each rotation in \(\pmb{\Theta}'_A\).
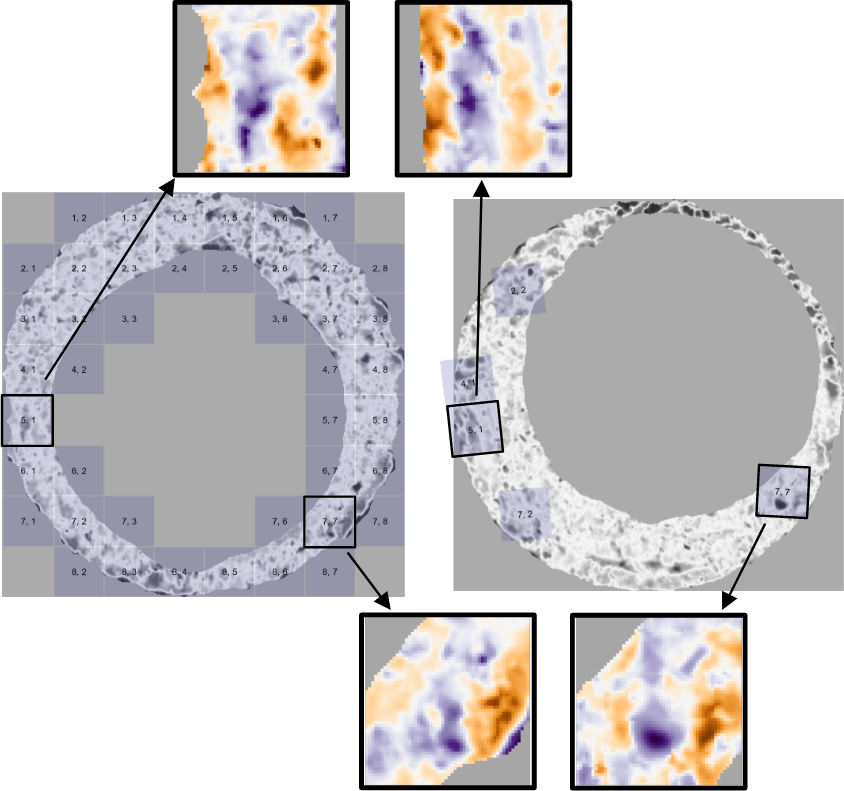
Figure 4.4: Estimated registrations of cells from a non-match pair of cartridge cases. A source scan (left) is separated into an \(8 \times 8\) grid of cells. We exclude cells containing only missing values (visualized here as gray pixels). Each source cell is compared to a target scan (right) to estimate where it aligns best. We show a handful of cells at their estimated alignment in the target scan and magnify the surfaces captured by cell pairs 5, 1 and 7, 7. Although the cartridge case pair is non-matching, we note that there are similarities in the surface markings for these cell pairs.
Figure 4.4 shows the estimated registrations of cells between two non-match cartridge cases. We magnify the surface values captured by cell pairs 5, 1 and 7, 7 and note the similarities in the surface values; for example, the dark purple region in the middle of the cell 7, 7 pair.
Just as with the whole-scan registration, we calculate the pairwise-complete correlation between each cell \(A_t\) and a matrix \(B_{\theta,t}^*\) of the same size extracted from \(B^*_{\theta}\) after translating by \([m^*_{A,\theta},n^*_{A,\theta}]\). From this we obtain a set of pairwise-complete correlations for each cell and rotation: \(\{cor_{A,t,\theta} : t = 1,...,T_A, \theta \in \pmb{\Theta}'_A\}\).
We repeat Cell-Based Comparison Algorithm and the pairwise-complete correlation calculation using \(B\) as the source scan and \(A^*\) as the target, resulting in cell-based registration set \(\pmb{F}_B\) and pairwise-complete correlations \(\{cor_{B,t,\theta} : t = 1,...,T_B, \theta \in \pmb{\Theta}'_B\}\).
For \(d = A,B\) and \(t = 1,...,T_d\), define the cell-wise maximum pairwise-complete correlation as:
\[ cor_{d,t} = \max_{\theta} \{cor_{d,t,\theta} : \theta \in \pmb{\Theta}'_d\} \]
We compute two features, the average and standard deviation of the cell-based pairwise-complete correlations, using the correlation data:
\[\begin{align*} \overline{cor}_{\text{cell}} &= \frac{1}{T_A + T_B} \sum_{d \in \{A,B\}} \sum_{t=1}^{T_d} cor_{d,t} \\ s_{cor} &= \sqrt{\frac{1}{T_A + T_B - 1} \sum_{d \in \{A,B\}} \sum_{t=1}^{T_d} (cor_{d,t} - \overline{cor}_{\text{cell}})^2} \end{align*}\]
We expect \(\overline{cor}_{\text{cell}}\) and \(s_{cor}\) to be large for truly matching cartridge case pairs relative to non-matching pairs.
For \(d = A,B\) and \(t = 1,...,T_d\), define the per-cell estimated translations and rotation as: \[\begin{align*} \theta^*_{d,t} &= \arg \max_{\theta} \{CCF_{\max,d,t,\theta} : \theta \in \pmb{\Theta}'_d\} \\ m^*_{d,t} &= m^*_{\theta^*_{d,t},d,t} \\ n^*_{d,t} &= n^*_{\theta^*_{d,t},d,t} \end{align*}\]
We compute the standard deviation of the cell-based estimated registrations using the estimated translations and rotations:
\[\begin{align*} s_{\theta^*} = \sqrt{\frac{1}{T_A + T_B - 1} \sum_{d \in \{A,B\}} \sum_{t=1}^{T_d} (\theta^*_{d,t} - \bar{\theta}^*)^2} \\ s_{m^*} = \sqrt{\frac{1}{T_A + T_B - 1} \sum_{d \in \{A,B\}} \sum_{t=1}^{T_d} (m^*_{d,t} - \bar{m}^*)^2} \\ s_{n^*} = \sqrt{\frac{1}{T_A + T_B - 1} \sum_{d \in \{A,B\}} \sum_{t=1}^{T_d} (n^*_{d,t} - \bar{n}^*)^2} \end{align*}\]
where
\[\begin{align*} \bar{m}^* &= \frac{1}{T_A + T_B} \sum_{d \in \{A,B\}}\sum_{t=1}^{T_d} m^*_{d,t} \\ \bar{n}^* &= \frac{1}{T_A + T_B} \sum_{d \in \{A,B\}} \sum_{t=1}^{T_d} n^*_{d,t} \\ \bar{\theta}^* &= \frac{1}{T_A + T_B} \sum_{d \in \{A,B\}} \sum_{t=1}^{T_d} \theta^*_{d,t}. \end{align*}\]
We expect \(s_{\theta^*}, s_{m^*},s_{n^*}\) to be small for truly matching cartridge case pairs relative to non-matching pairs.
From the full-scan and cell-based registration procedures, we obtain six features summarized in Table 4.1.
| \(cor_{\text{full}}\) | Full-scan pairwise-complete correlation |
| \(\overline{cor}_{\text{cell}}\) | Average cell-based pairwise-complete correlation |
| \(s_{cor}\) | Standard deviation of the cell-based pairwise-complete correlations |
| \(s_{m^*}\) | Standard deviation of the cell-based vertical translaitons (in microns) |
| \(s_{n^*}\) | Standard deviation of the cell-based horizontal translations (in microns) |
| \(s_{\theta^*}\) | Standard deviation of the cell-based rotations (degrees) |
4.3.2.4 Density-Based Features
We wish to identify when multiple cells agree on, or cluster around, a particular registration value. However, pursuant with the notion that only certain regions of matching cartridge cases contain distinctive markings, it is unreasonable to assume and empirically rare that all cells agree on a single registration. In fact, it is common for many cells to disagree on a registration. For example, the left scatterplot in Figure 4.5 shows the per-cell estimated translations \([m^*_{A,t,\theta}, n^*_{A,t,\theta}]\) when scan \(A\) is used as source and \(B^*\) as target rotated by \(\theta = 3^\circ\). The right scatterplot shows the per-cell estimated translations with the roles of \(A\) and \(B^*\) reversed for \(\theta = -3^\circ\). We see distinctive clusters, the black points, in both plots among many noisy, gray points. The task is to isolate the clusters amongst such noise.
We use the Density-Based Spatial Clustering of Applications with Noise (DBSCAN) algorithm proposed by Ester et al. (1996) to identify clusters. Compared to other clustering algorithms such as k-means (MacQueen 1967), DBSCAN does not require a pre-defined number of expected clusters. Instead, the algorithm forms clusters if the number of points within an \(\epsilon > 0\) distance of a point exceeds some pre-defined threshold, \(minPts > 1\). If a point does not belong to a cluster, then DBSCAN labels that point as “noise.” In Figure 4.5, we use DBSCAN with \(\epsilon = 5\) and \(minPts = 5\) to identify clusters of size 14 and 13, respectively, visualized as black points. These cluster sizes suggest that the scans match. Additionally, the mean cluster centers are approximately opposites of each other: \((\hat{m}_A,\hat{n}_A,\hat{\theta}_A) \approx (16.9, -16.7, 3^\circ)\) when \(A\) is used as source compared to \((\hat{m}_B,\hat{n}_B,\hat{\theta}_B) \approx (-16.2, 16.8, -3^\circ)\) when \(B^*\) is used as source. This provides further evidence of a match.
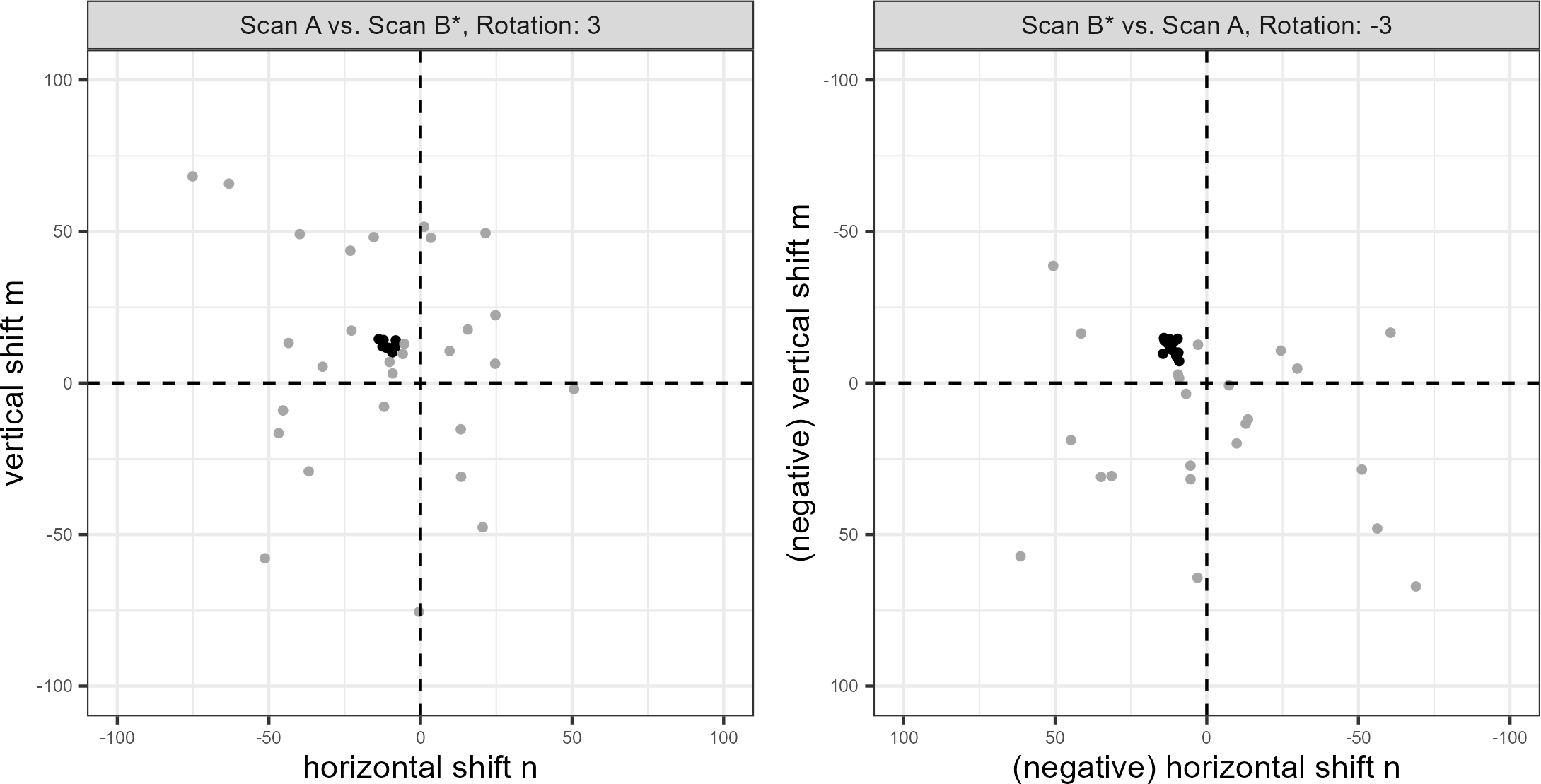
Figure 4.5: Cluster assignments based on the Density Based Spatial Clustering with Applications to Noise (DBSCAN) algorithm for estimated translations in two comparison directions. Using scan \(A\) as source results in a cluster of size 14 (left) compared to 13 when scan \(B^*\) is used as source (right). Noting the reversed axes in the right plot, we see that the clusters are located approximately opposite of each other. Points are jittered for visibility.
To calculate the density-based features, we first use a 2D kernel density estimator (Venables and Ripley 2002) to identify the rotation \(\hat{\theta}_d\) at which the per-cell translations achieve the highest density. Next, we compute clusters using the DBSCAN algorithm amongst the estimated translations \(\{(m^*_{d,t,\hat{\theta}_d},n^*_{d,t,\hat{\theta}_d}) : t = 1,...,T_d\}\) like those shown in Figure 4.5.1 Let \(\pmb{C}_d\) denote the set of cells in the DBSCAN cluster. We treat the mean cluster centers as the estimated translations \([\hat{m}_d,\hat{n}_d]\).
We calculate four features from the density-based clustering procedure: average DBSCAN cluster size \(C\), the DBSCAN cluster indicator \(C_0\), and the root sum of squares of the density-estimated registrations \((\Delta_\theta, \Delta_{\text{trans}})\) defined as:
\[\begin{align*} C &= \frac{1}{2}\left(|\pmb{C}_A| + |\pmb{C}_B|\right) \\ C_0 &= I(|\pmb{C}_A| > 0 \text{ and } |\pmb{C}_B| > 0)\\ \Delta_\theta &= |\hat{\theta}_A + \hat{\theta}_B| \\ \Delta_{\text{trans}} &= \sqrt{(\hat{m}_A + \hat{m}_B)^2 + (\hat{n}_A + \hat{n}_B)^2} \end{align*}\]
where \(|\pmb{C}_d|\) denotes the cardinality of \(\pmb{C}_d\) and \(I(\cdot)\) is the identity function equal to 1 if the predicate argument “\(\cdot\)” evaluates to TRUE and 0 otherwise. We use both \(C\) and \(C_0\) because of potential missingness in the values of \(C\) if no cluster is identified. Missing \(C\) values are imputed using the median non-missing value when fitting classifiers, so the missingness information is retained in \(C_0\).
For truly matching cartridge case pairs, we expect \(C\) to be large, \(C_0\) to be 1, and \(\Delta_\theta, \Delta_{\text{trans}}\) to be small relative to non-matching pairs. We obtain four density-based features summarized in Table 4.2.
| \(C\) | Average DBSCAN cluster size |
| \(C_0\) | DBSCAN cluster indicator |
| \(\Delta_{\theta}\) | Root sum of squares of the cluster-estimated translations (in microns) |
| \(\Delta_{\text{trans}}\) | Root sum of squares of the cluster-estimated translations (in microns) |
4.3.2.5 Visual Diagnostic Features
The final set of features we calculate are based on visual diagnostic tools described in Chapter 3. These numerical features quantify the qualitative observations one can make from the diagnostics. We provide a broad summary of the visual diagnostics features here, but we encourage the reader to see Chapter 3 to learn more.
To construct the visual diagnostics, we perform element-wise operations on two matrices. For the full scan comparisons, we perform these operations on the matrices \(A\) and \(B^*\), which is the aligned version of \(B\) after applying the image registration algorithm. We introduce the visual diagnostics in the context of the full scan comparisons, but they generalize smoothly to the case of cell comparisons as well.
For a matrix \(X \in \mathbb{R}^{k \times k}\) and Boolean-valued condition matrix \(cond: \mathbb{R}^{k \times k} \to \{TRUE,FALSE\}^{k \times k}\), we define an element-wise filter operation \(\mathcal{F}: \mathbb{R}^{k \times k} \to \mathbb{R}^{k \times k}\) as:
\[\begin{align*} \mathcal{F}_{cond}(X) = (f_{ij})_{1 \leq i,j \leq k} = \begin{cases} x_{ij} &\text{if $cond$ is $TRUE$ for element $i,j$} \\ NA &\text{otherwise} \end{cases} \end{align*}\]
For example, \(\mathcal{F}_{|A - B^*| > \tau}(A)\) contains elements of matrix \(A\) where the pair of scans \(A\) and \(B^*\) deviate by at least \(\tau > 0\). Surface values in \(A\) and \(B^*\) that are “close,” meaning within \(\tau\) distance, to each other are replaced with \(NA\) in this filtered matrix.
We compute features based on the elements of the \(cond\) matrix. First, we consider the ratio between the number of \(TRUE\) and \(FALSE\) elements in the matrix \(|A - B^*| \leq \tau\), where \(TRUE\) values correspond to elements of \(A\) and \(B^*\) within \(\tau\) distance of each other. The definition of this ratio is given by Equation (3.1).
Figure 3.11 in Chapter 3 shows an example of this ratio for two matching \(A = K013sA1\) and \(B = K013sA2\). The value of the “similarities vs. differences ratio” is 2.84 using a filter threshold of \(\tau = 1\) micron If we consider the \(TRUE\) and \(FALSE\) elements of the \(|A - B^*| \leq \tau\) matrix as the elements of \(A\) and \(B^*\) that are most “similar” and “different” then we can interpret this value to mean that there are 2.84 times as similarities as there are differences.
Because we perform comparisons in both directions \(d = A,B\), we end up with two similarities vs. differences ratio values. We compute the arithmetic mean between these two values to obtain a summary feature for the cartridge case pair as a whole: \[ r_{\text{full}} = \frac{1}{2}(r_A + r_B). \] We assume that the full-scan similarities vs. differences ratio will be larger for matching cartridge case pairs than non-matches.
As another source of features, we consider the size of \(TRUE\)-valued neighborhoods in the \(cond\) matrix \(|A - B^*| > \tau\), which is the logical complement of the \(cond\) matrix used to compute \(r_{\text{full}}\). An example of one such matrix can be seen on the left side of 3.12. We consider each neighborhood as a set of adjacent elements, \(S\), that all have the same value. Two elements are “adjacent” if one of their indices differs by 1 (this is a 4-neighbor or “Rook’s” scheme). We use a connected components labeling algorithm (Hesselink, Meijster, and Bron 2001) to identify neighborhoods that all have the value \(TRUE\) in \(|A - B^*| > \tau\). The middle of 3.12 shows an example of neighborhood regions distinguished by fill color. Using this procedure in both comparison directions, we obtain multiple neighborhoods that we distinguish notationally using subscripts: \(\pmb{S}_d = \{S_{d,1}, S_{d,2}, ..., S_{d, l} : l = 1,...,L_d\}\) where \(L_d\) is the total number of labeled \(TRUE\)-valued regions in direction \(d \in \{A,B\}\).
Considering the size of each labeled region on the right side of Figure 3.12, we see that the distribution is heavily right-skewed with the majority of comparisons being relatively small - less than 1,000 square microns. If we associate the \(TRUE\) values of \(|A - B^*| > \tau\) with elements where \(A\) and \(B^*\) are the most “different,” then it is reasonable to assume that the size of individual \(TRUE\)-valued regions would be small for a matching pair. In other words, that there wouldn’t be large regions where \(A\) and \(B^*\) are different if they truly match.
To compute numerical features based on this assumption, we consider the average and standard deviation of the blob sizes across the two comparison directions:
\[\begin{align*} \overline{|S|}_{\text{full}} &= \frac{1}{L_A + L_B} \sum_{d \in \{A,B\}} \sum_{l=1}^{L_d} |S_{d,l}| \\ s_{\text{full},|S|} &= \sqrt{\frac{1}{L_A + L_B - 1} \sum_{d \in \{A,B\}} \sum_{l=1}^{L_d} (|S_{d,l}| - \overline{|S|}_{\text{full}})^2} \end{align*}\]
where \(|S_{d,l}|\) is the number of elements (cardinality) in set \(S_{d,l}\), \(l = 1,...,L_d\) and \(d = A,B\). We assume that the average and standard deviation of the full-scan neighborhood sizes will be small for matching pairs compared to non-matching pairs.
As a final source of features, we consider the correlation \(cor_{d,\text{full},\text{diff}}\) between the elements of the matrices \(\mathcal{F}_{|A - B^*| > \tau}(A)\) and \(\mathcal{F}_{|A - B^*| > \tau}(B^*)\) for \(d = A\) and \(\mathcal{F}_{|A^* - B| > \tau}(A^*)\) and \(\mathcal{F}_{|A^* - B| > \tau}(B)\) for \(d = B\). If \(A\) and \(B\) are truly matching, then we might assume that differences in the height values occur merely because of variability in the amount of contact between the cartridge case and breech face across multiple fires of a single firearm. Figure 3.13 shows an example of the “filtered differences” between two cells \(\mathcal{F}_{|A_t - B_t^*| > \tau}(A_t)\) and \(\mathcal{F}_{|A_t - B_t^*| > \tau}(B_t^*)\). Although the surface values in the cell on the right appear to be shifted up relative to the values from the cell on the left, as evidenced by the generally darker shades of orange, the trends in the surface values are similar. This is reflected in the relatively high correlation value of 0.84 between these two filtered cells.
Similar to the other features, we use the average “differences correlation” value \(cor_{d,\text{full},\text{diff}}\) across the two comparison directions as a feature:
\[ cor_{\text{full},\text{diff}} = \frac{1}{2}\left(cor_{A,\text{full},\text{diff}} + cor_{B,\text{full},\text{diff}}\right). \]
We assume that the full-scan differences correlation will be large for matches compared to non-matches.
So far, we’ve discussed visual diagnostic features for full scan comparisons. We also compute summary features based on the visual diagnostics applied to the cell-based comparisons. Letting \(A_t\) and \(B_t^*\) denote a pair of aligned cells from scans \(A\) and \(B^*\), respectively, we extend the full scan notation introduced above by adding \(t\) subscripts.
We compute the average and standard deviation of the cell-based similarities vs. differences ratio values: \[\begin{align*} \bar{r}_{\text{cell}} &= \frac{1}{T_A + T_B} \sum_{d \in \{A,B\}} \sum_{t = 1}^{T_d} r_{d,t} \\ s_{\text{cell}, r} &= \sqrt{\frac{1}{T_A + T_B - 1} \sum_{d \in \{A,B\}} \sum_{t = 1}^{T_d} (r_{d,t} - \bar{r}_{\text{cell}})^2}, \end{align*}\]
We also calculate the per-cell average and standard deviation labeled neighborhood size: \[\begin{align*} \overline{|S|}_{d,t} &= \frac{1}{L_{d,t}} \sum_{l=1}^L |S_{d,t,l}| \\ s_{d,t,|S|} &= \sqrt{\frac{1}{L_{d,t} - 1} \sum_{l=1}^{L_{d,t}} (|S_{d,t,l}| - \overline{|S|}_{\text{cell},d,t})^2}, \end{align*}\] and average these values to features for the pair as a whole: \[\begin{align*} \overline{|S|}_{\text{cell}} &= \frac{1}{T_A + T_B} \sum_{d \in \{A,B\}} \sum_{t=1}^{T_d} \overline{|S|}_{d,t} \\ \bar{s}_{\text{cell},|S|} &= \frac{1}{T_A + T_B} \sum_{d \in \{A,B\}} \sum_{t=1}^{T_d} s_{d,t,|S|}. \end{align*}\] We assume that the average cell-wise neighborhood size and the average standard deviation of the cell-wise neighborhood sizes will be small for matching pairs relative to non-match pairs.
Finally, we compute the average cell-based differences correlation across all cells in both comparison directions: \[\begin{align*} \overline{cor}_{\text{cell},\text{diff}} &= \frac{1}{T_A + T_B} \sum_{d \in \{A,B\}} \sum_{t=1}^{T_d} cor_{d,t,\text{diff}}. \end{align*}\]
Table 4.3 summarizes the nine features based on visual diagnostics. A deeper exploration of these features can be found in Chapter 3. This concludes our explanation of the ACES feature set. Next, we use the 19 ACES features to train and test classifier models.
| \(cor_{\text{full},\text{diff}}\) | Full-scan differences correlation |
| \(\overline{cor}_{\text{cell},\text{diff}}\) | Average cell-wise differences correlation |
| \(r_{\text{full}}\) | Full-scan similarities vs. differences ratio |
| \(\bar{r}_{\text{cell}}\) | Average cell-based similarities vs. differences ratio |
| \(s_{\text{cell}, r}\) | Standard deviation of the cell-based similarities vs. differences ratio |
| \(\overline{|S|}_{\text{full}}\) | Average full-scan neighborhood size |
| \(s_{\text{full},|S|}\) | Standard deviation of the full-scan neighborhood sizes |
| \(\overline{|S|}_{\text{cell}}\) | Average cell-wise neighborhood sizes |
| \(\bar{s}_{\text{cell},|S|}\) | Average standard deviation of the cell-wise neighborhood sizes |
4.3.3 Scoring
We use a data set of 510 cartridge cases fired from 25 firearms. We randomly split the data into 10 firearms for training and 15 firearms for testing. This resulted in a training data set of 210 cartridge cases, \(\binom{210}{2} = 21,945\) pairwise comparisons, and a testing set of 300 cartridge cases, \(\binom{300}{2} = 44,850\) pairwise comparisons. Because we consider every pairwise comparison between these scans, there is a relatively large class imbalance between matches and non-matches in these data sets. Specifically, non-matching comparisons make up 19,756 of the 21,945 (90.0%) training comparisons and 41,769 of the 44,850 (93.1%) testing comparisons.
We use 10-fold cross-validation repeated thrice (Kuhn 2022) to train two binary classifiers based on a logistic regression and a random forest (Breiman 2001; Liaw and Wiener 2002). These models predict the probability that a pair of cartridge cases match. Then, the model classifies the pair as a match or non-match depending on whether the match probability exceeds a set threshold. On top of the tunable parameters of each model (e.g., the DBSCAN parameters \(\epsilon\) and \(minPts\)), we treat this threshold as a parameter to be optimized.
Models trained to maximize accuracy on imbalanced data often exhibit a “preference” for classifying new observations as the majority class (Fernández et al. 2018), which in our case are non-matches. An optimization criterion commonly used for imbalanced data is to select the model that maximizes the area under the Receiver Operating Characteristic (ROC) curve, which measures the performance of a model under different threshold values (James et al. 2013). The model that maximizes this area, commonly abbreviated AUC, is one that performs best under a variety of threshold values relative to the other models - this consistency is a desired trait. Using the ROC curve, we choose the match probability threshold that balances the true negative and true positive (equivalently, the false positive and false negative) rates on the training data.
Once we have a trained model, we use it to predict the match probability and classify a new cartridge case pair. However, rather than referring to the number returned by the trained model as a “probability,” which implicitly assumes a homogeneous source population between the training and test cartridge cases, we simply call the number a “score” where larger values correspond with more similar cartridge cases. We compute this score for the pairwise comparisons in the test data as a means of comparing the generalizability of the various models. The following section details the results of this cross-validation training/testing procedure.
4.4 Results
4.4.1 ROC Curves
First, we consider results from the training procedure. 4.6 shows the resulting ROC curves for four classifier models trained on the training data set. We consider training the logistic regression (LR) and random forest (RF) models under two feature sets: a subset of the full ACES feature set consisting of the Cluster Indicator feature \(C_0\) and the six registration-based features summarized in Table 4.1 vs. all 19 ACES features. We consider the “\(C_0\) + Registration” subset of features to represent the features used in Congruent Matching Cells methods [Song (2013); zhang_convergence_2021].
The ROC curves allow us to visually compare the behavior of these four classifiers under various score thresholds where curves closer to the top-left corner are preferred. Broadly speaking, the four models perform comparably as evidenced by the similar curves on the right side of 4.6. The left side shows a zoomed-in version of the top left corner of plot, which makes it easier to compare the different curves. Visually, we see that the choice of feature group has a larger impact on the outcome classification behavior than the choice between the logistic regression or random forest models.
To numerically compare the four models, we compute the area under the ROC curve (AUC) as well as the score threshold (Thresh.) that balances the false negative and false positive rates (the equal error rate or EER). The AUC for the All ACES logistic regression and random forest classifiers are higher than the AUC of the two classifiers trained on the \(C_0\) + Registration feature set. Each model has a different score threshold that yields the equal error rate, which we visualize as points along the four ROC curves in 4.6. We use these thresholds to compute both the training and test classification results summarized below. We see that the All ACES, logistic regression model has the lowest equal error rate out of the four models with the All ACES, random forest model a close second.
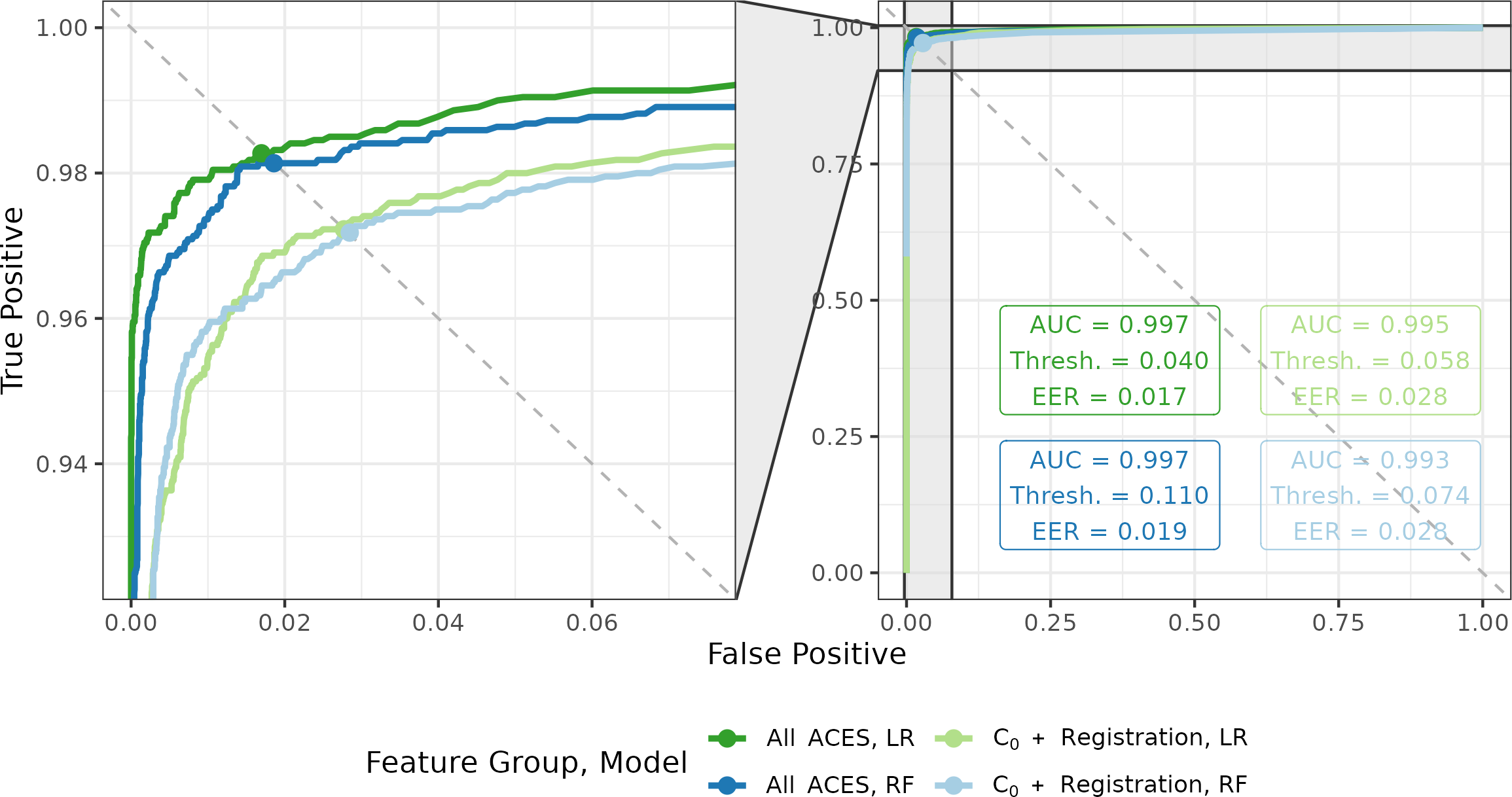
Figure 4.6: ROC curves for logistic regression (LR) and random forest (RF) models trained using two feature sets - all 19 ACES features vs. a subset of seven ACES features. On the left, we zoom into the top-left corner of the ROC curve plot to better distinguish between the four curves. We see that the models trained on the full ACES feature set have higher area under the curve (AUC) and lower equal error rate (EER) values than on the subset. We also show the score classification cutoffs (Thresh.) used for each of the four models to achieve the equal error rate values.
4.4.2 Optimized Model Comparison
Figure 4.7 summarizes the training and testing accuracy, true negative and true positive rates for five binary classifiers. We distinguish between the training and testing results using gray and black points/line segments, respectively, which allows us to assess the generalizability of the various models. The conclusions drawn from Figure 4.7 are intended to primarily be qualitative and comparative across models. Table 4.6 and Table 4.7 in the Appendix provide a numerical summary of these results.
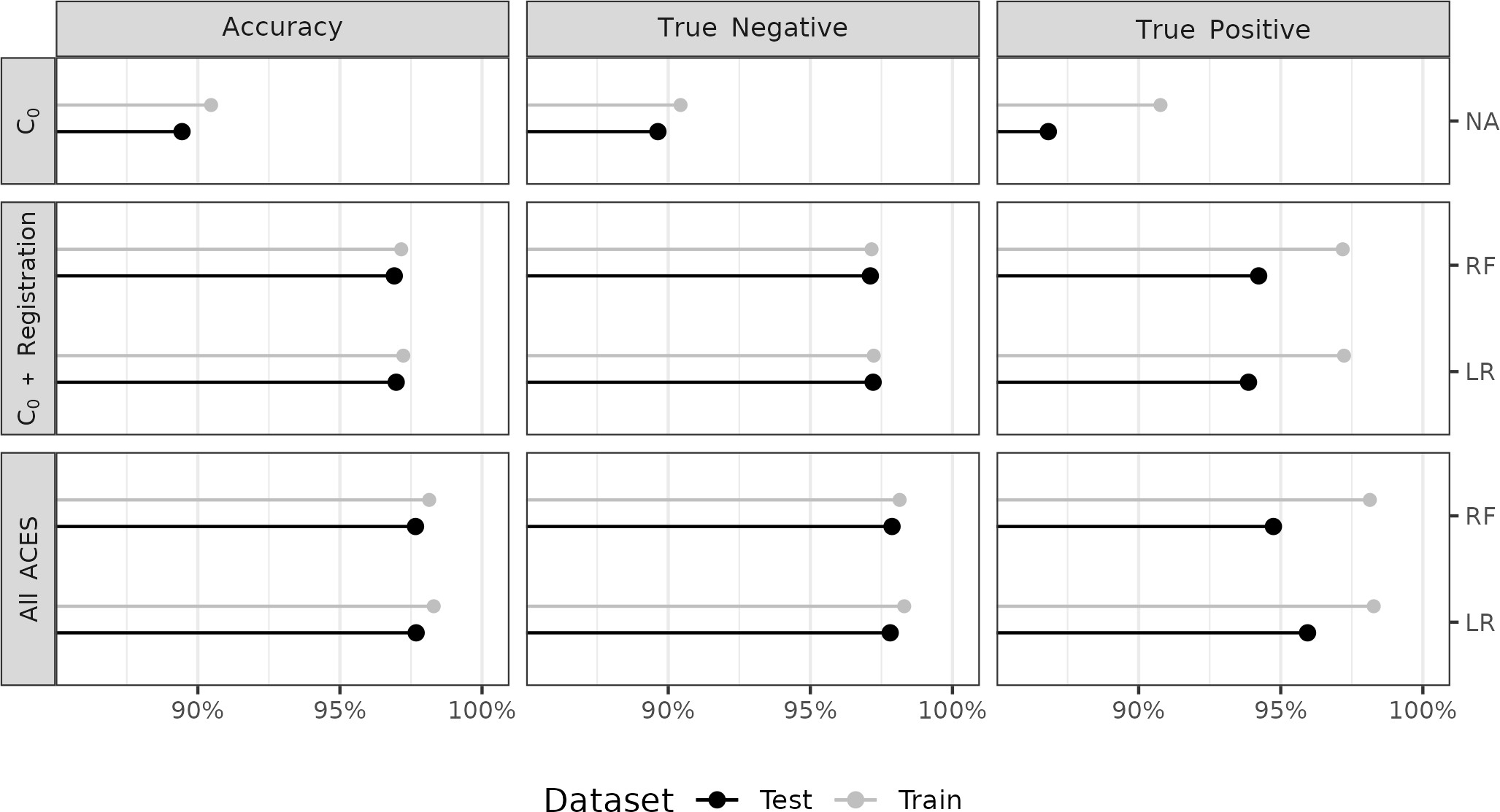
Figure 4.7: We summarize classification accuracy, true negative, and true positive rates for both the training and testing results, represented as gray and black points/lines respectively, for five binary classifier models. Our primary interest is the test data results, but visualizing the training data results allows us to assess the generalizability of the models after training. In the first row, we consider a classifier based on a single feature, the Cluster Indicator feature \(C_0\), as a baseline. The remaining rows show results from training/testing classifiers based on a random forest (RF) and logistic regression (LR) under various feature sets and optimization critieria. The second row shows results based on a subset of seven features from the ACES feature set while the third row shows results using all 19 ACES features.
We first compare the training and testing results across the five models and three columns in Figure 4.7. In general, the true negative rates based on the test data are slightly lower than those of the training data indicating that the models’ ability to distinguish between non-matching comparisons generalizes well to the testing data. In contrast, the true positive rates tend to be lower for the test data compared to the training data across the various models, which indicates a potential difference between the training and testing data. As we discuss below, there is a single firearm among the 15 test firearms that contributes the majority of false negative (misclassified match) test classifications. Despite lower true positive rates, the overall accuracy between the training and testing sets are comparable due to the large class imbalance between matching and non-matching comparisons in both.
In the first row, we consider a baseline classifier based solely on the Cluster Indicator feature \(C_0\). Namely, if the DBSCAN algorithm finds clusters in the cell-based translations from both directions of a cartridge case comparison, then that pair is classified as a match. This is analogous to the classification rule used in Zhang et al. (2021). We optimized this \(C_0\)-based classifier by choosing the DBSCAN parameters \(\epsilon\) and \(minPts\) that resulted in the most balanced training true negative and true positive rates, resulting in \(\epsilon = 15\) and \(minPts = 8\). The optimized \(C_0\)-based classifier performs considerably worse across the three measures compared to the other models with test accuracy 89.44%, true negative rate 89.64%, and true positive rate 86.82%.
The second row of Figure 4.7 summarizes results from training the two classifier models on a subset of the full ACES feature set consisting of the Cluster Indicator feature \(C_0\) and the six registration-based features summarized in Table 4.1. We consider this subset of features to represent the features used in Congruent Matching Cells methods (Song 2013; Zhang et al. 2021). In general, we see that the logistic regression (LR) and random forest (RF) models perform comparable to each other in accuracy, true negative, and true positive rates. Despite the fact that the models in the second and third rows were selected based on balancing the training true negative and true positive rates, we note that these rates for the test data are not as well-balanced; namely, the true negative rates still tend to be larger than the true positive rates. Below, we explore this discrepancy by analyzing the contribution of various test firearms towards the true positive rates.
The third row of Figure 4.7 summarizes the classification results based on using all 19 ACES features. If we compare the “\(C_0\) + Registration”-trained models in the second vs. the “All ACES”-trained models in the third row, we see that the addition of the other ACES features leads to improved test true negative and true positive rates (and consequently overall accuracy) with the most noticeable gains observed in the true positive rate. Across all five models, the All ACES-trained logistic regression model has the largest overall test accuracy and true positive rates of 97.68% and 95.94%, respectively. The All ACES-trained random forest model has the largest overall true negative rate of 97.87%, although the All ACES, logistic regression model is a close second at 97.81% (see Table 4.7 for more details).
4.4.3 Similarity Score Investigation
While it’s useful to consider the accuracy, true negative, and true positive rates to compare various models, forensic examiners would likely not use the binary classification returned by a model in casework. Instead, they would consider the match probability predicted by the model as a similarity score and incorporate it into their decision-making process. As such, we also consider the distribution of the predicted similarity scores for matching and non-matching comparisons. Figure 4.8 shows a dot plot of the predicted similarity scores for the 41,769 non-match and 3,181 match comparisons in the test set. Specifically, these probabilities are predicted by the logistic regression model selected to maximize the AUC based on the full ACES feature set. As we expect, few non-match comparisons have large similarity scores, which justifies the low false positive rate observed in Figure 4.7. However, there is a surprising number of matching comparisons that also have a low match probability.
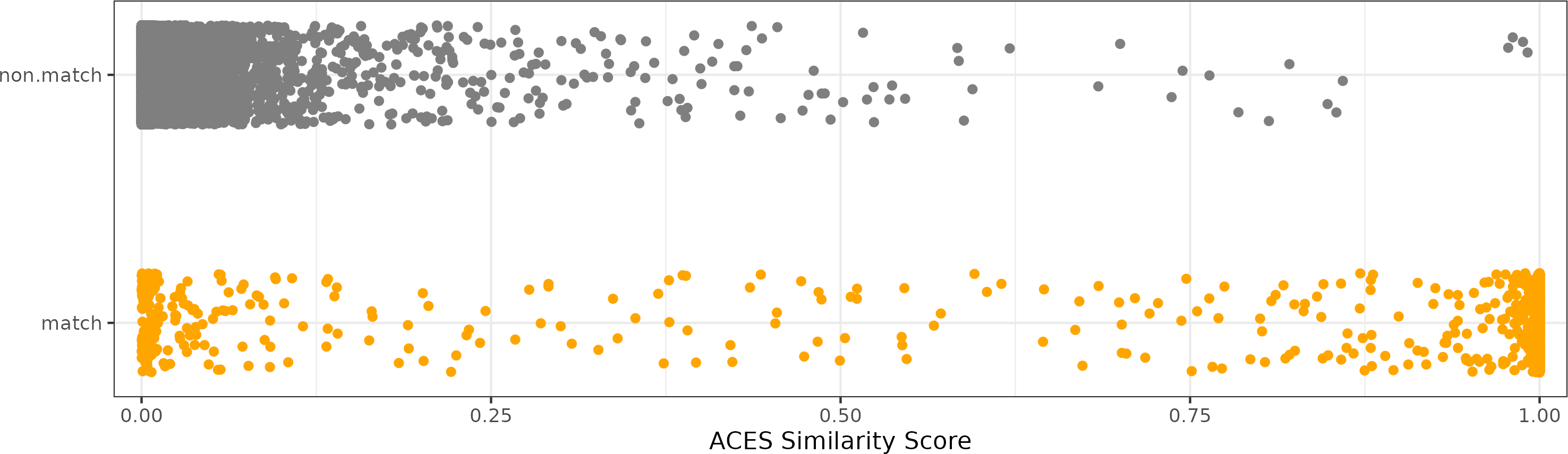
Figure 4.8: A dot plot of the predicted similarity scores for the non-match and match comparisons in the test set based on a logistic regression model. As we expect, the non-match comparisons tend to have a low match probability. However, we see that there are many matching comparisons that also have a low match probability.
To explain the matching comparisons with low similarity scores, we visualize in Figure 4.9 the predicted similarity scores for matching test comparisons distinguished by the 15 test firearm ID. We see that the firearm T has far more matching comparisons with low similarity scores compared to the other 14 test firearms. This is further underscored by the right side of the Figure 4.9, which shows the ratio of misclassifications to total comparisons for every pair of test firearms based on the same logistic regression model used in Figure 4.8. The main diagonal shows the false negative misclassifications while the off-diagonal shows the false positives. We use blank tiles for comparisons where 0 misclassifications occurred. We see that the false negative rate for firearm T of 27.1% is far greater than that of other firearm pairs. The 95 false negative firearm T comparisons comprise 76% of all 125 false negative test comparisons and about 3% of all 3,181 matching test comparisons. In sum, the model performs distinctly worse at identifying matching comparisons from firearm T compared to the other firearms, which partially explains the lower test true positive rates noted in Figure 4.7. Upon visual inspection of the scans from firearm T, we noted a lack of consistent markings on their surfaces, which isn’t the case for scans from other test firearms.
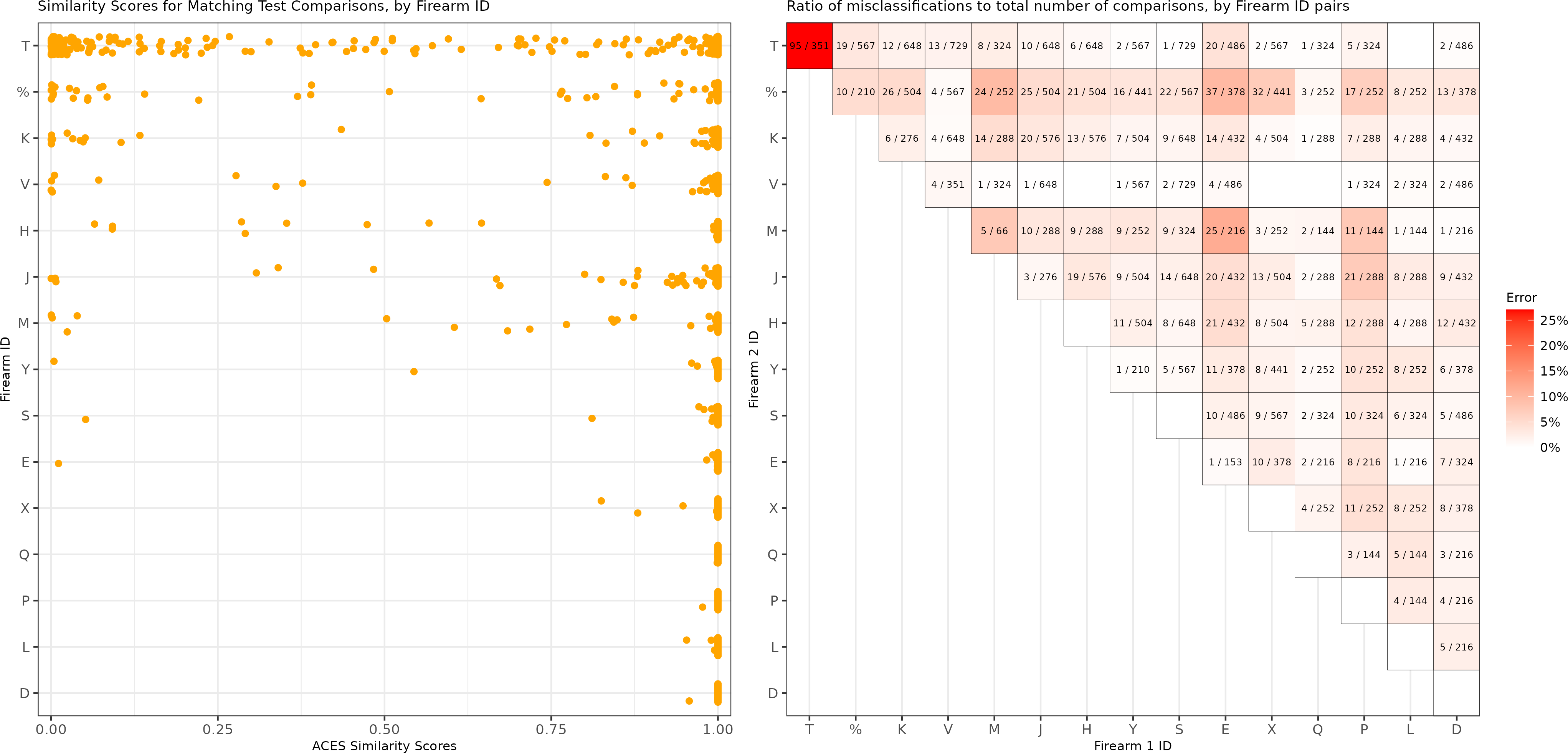
Figure 4.9: (Left) A dot plot of the predicted similarity scores for the match comparisons in the test set based on a logistic regression model, separated by firearm. We see that firearm T has more matching comparisons with low similarity scores than the other test firearms. (Right) Misclassifications divided by total number of pairwise comparisons for each pair of test firearms based on the same logistic regression model. We do not show comparisons with 0 misclassifications. We note that the proportion of misclassified matching comparisons from firearm T of 27.1 percent is much higher than that of other comparisons.
4.4.4 Feature Importance
Finally, we consider the relative importance of the 19 ACES features by fitting 10 replicate random forests using the full ACES feature set with fixed random seeds. For each replicate, we measure a variable’s importance using the Gini Index, which measures the probability of making a misclassification for a given model (Hastie, Tibshirani, and Friedman 2001). A larger decrease in the Gini Index corresponds with higher importance. Figure 4.10 shows the distribution of the mean Gini Index decrease for the 19 ACES features. Noting the log scale on which these points are plotted, we see that the most important features consist of a combination of density-based features \(C_0\), \(C\), and \(\Delta_{\text{trans}}\) and registration-based correlation features \(\overline{\text{cor}}_{\text{cell}}\) and \(\text{cor}_{\text{full}}\). In general, the visual diagnostic features tend to have lower importance scores compared the registration and density-based features. We discuss the sensitivity of these importance scores to various algorithm parameter choices in the next section.
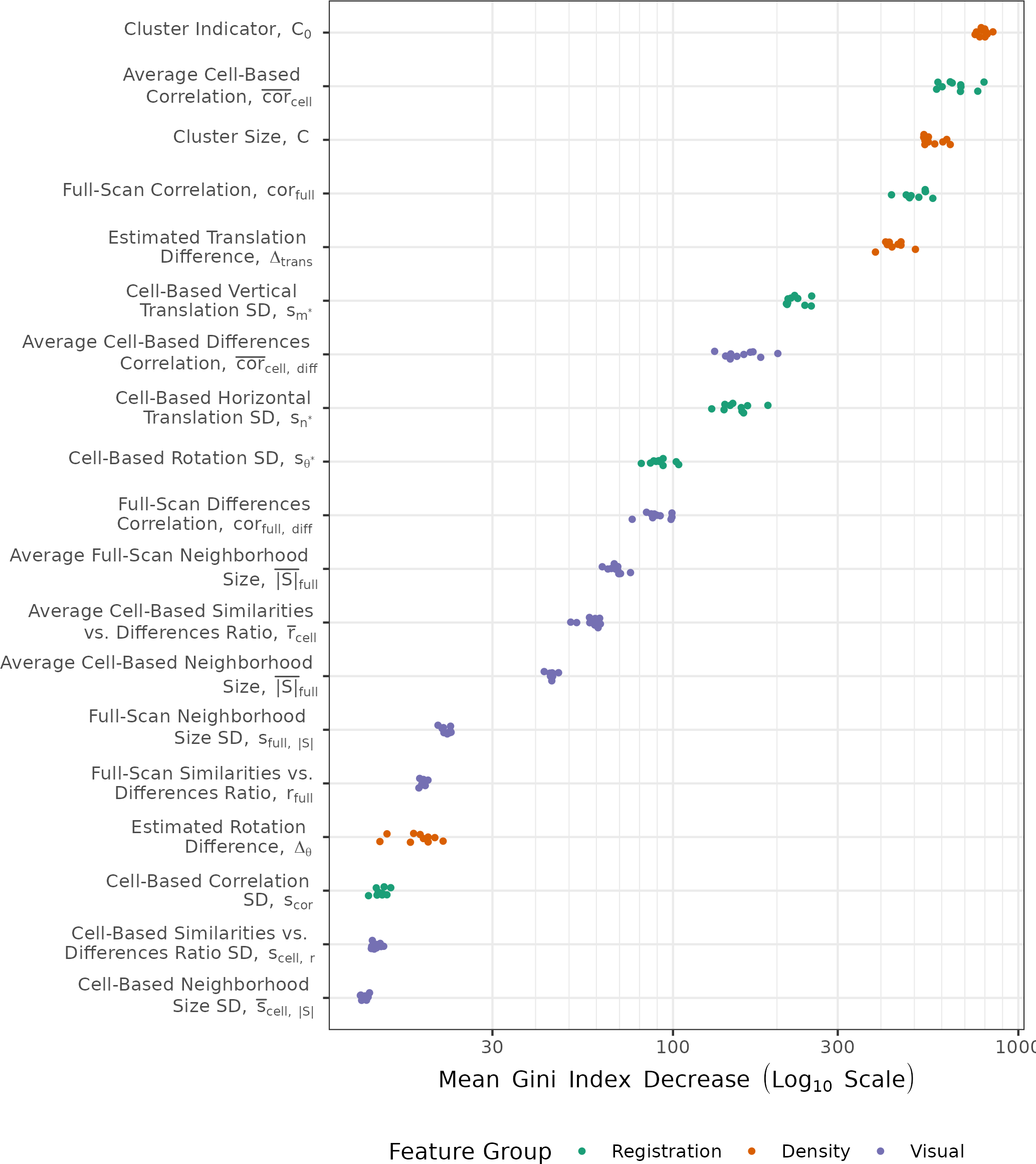
Figure 4.10: Variable importance measures from fitting a random forest to the training data set, repeated 10 times under various random seeds. The top features consist of density-based features \(C\) and \(C_0\) and registration-based features \(\overline{\text{cor}}_{\text{cell}}\) and \(\text{cor}_{\text{full}}\). We plot points on a log scale and vertically jitter them for visibility.
4.5 Discussion
4.5.1 Comparison to CMC Methodology
We use a \(C_0\)-based classifier as a baseline because it is analogous to the classification rule proposed in Zhang et al. (2021). Similarly, the cell-based registration features are based on the the same cell-based comparison procedure used in Song (2013) and summarized in cell-based comparison. Together, we consider \(C_0\) and the registration-based features a fusion of previously proposed cartridge case similarity scoring algorithms. This is why we fit separate classifiers based on these features for the training and testing results shown in Figure 4.9. Table 4.4 summarizes the similarities between the ACES algorithm and the algorithms proposed in Zhang et al. (2021) and Song (2013). Another key difference between ACES and both of the previous algorithms is the training/testing procedure used to optimize and validate model parameters.
| Paper | Translation \(T_x, T_y\) (in pixels) | Rotation \(\theta\) (in degrees) | \(CCF_{\max}\) |
|---|---|---|---|
| Song (2013) | Use the cell-based comparison algorithm to estimate cell-based registrations | Call cells Congruent Matching Cells if their registrations are close to a reference value. Classify a cartridge case pair as a match if the CMC count is at least 6. | Compute six summative features based on full-scan and cell registrations. Use features in a classifier model. |
| Zhang et al. (2021) | Use DBSCAN algorithm to identify cells that reach a consensus registration. | Classify a cartridge case pair as a match if a DBSCAN cluster is identified. | Compute four numerical features based on DBSCAN clusters across both comparison directions. Use features in a classifier model. |
Table 4.5 shows the test classification error rates of the Congruent Matching Cells (CMC) algorithm proposed in Song (2013), the \(C_0\)-based classifier like the one proposed in Zhang et al. (2021), and the two ACES logistic regression models selected to balance the true negative and true positive rates and maximize the classification accuracy. We obtained the CMC results by applying the implementation available in the cmcR R package (Joe Zemmels, Hofmann, and VanderPlas 2022) on the same test data set used in the Results section. We used the optimization procedure described in Joseph Zemmels, VanderPlas, and Hofmann (2023) to select CMC parameters. The \(C_0\)-based error rates are the same as those shown in the first row of Figure 4.7. The ACES logistic regression models perform better than the other classifiers on this test data set, most notably when compared to the CMC method in identifying matching cartridge case pairs. Interestingly, the \(C_0\)-based classifier has a lower false negative error rate compared to the All ACES-trained, maximum accuracy logistic regression model, although it has a much higher false positive rate.
| Original Paper | Error | False Positive (%) | False Negative (%) |
|---|---|---|---|
| CMC Method | 3.9 | 2.3 | 25.8 |
| Only \(C_0\) feature | 9.5 | 9.6 | 9.2 |
| ACES LR | 2.3 | 2.2 | 3.8 |
Both the registration and density-based features aim to measure similarities between two cartridge case surfaces. These features embody the notion assumed in the CMC methodology that matching cartridge cases should have similar markings, so their cell-based correlations should be large and estimated registrations should agree. However, 4.4 demonstrates that even non-matching cartridge case pairs may share similar markings. We are bound to find similarities if that is all we look for, so it is worthwhile to also consider dissimilarities. The visual diagnostic features accomplish this by partitioning scans into similar and different regions. The similarities vs. differences ratio and labeled neighborhood size features measure how extreme the differences are between two scans while the differences correlation features determine whether there are similarities among the different regions.
This direct comparison of the surface values aligns with the Theory of Identification which says that an examination should involve the comparison of the “relative height or depth, width, curvature and spatial relationship” of cartridge case impressions (AFTE Criteria for Identification Committee 1992). Comparison algorithms like ACES will inevitably be used to augment the opinion of a forensic examiner, who may need to present algorithmic results to judges or juries as part of their expert testimony. As such, it is important that forensic examiners are able to interpret and explain the results of a comparison algorithm. The visual diagnostic features are useful for explaining the behavior of the algorithm in a manner that aligns with more traditional identification theory.
4.5.2 Sensitivity to Parameter Choice
When selecting the optimal models presented in 4.7, we performed a good deal of searching across various parameter choices. For example, given the relative importance of the density-based features illustrated in 4.10, we were interested in assessing the sensitivity of the various classifier models to DBSCAN parameter choice. 4.11 shows a heat map of AUC values for the four combinations of feature group and classifier model shown in 4.7 across a grid of DBSCAN parameter values \(\epsilon \in \{3,...,15\}\) and \(minPts \in \{3,...,10\}\). Darker tiles correspond with higher AUC values, which in turn are associated with more preferred models. We draw a black square around the specific \((\epsilon, minPts)\) values resulting in the maximum AUC for each of the models (which we also show in 4.6. Interestingly, we see that all four models achieve optimum AUC for smaller values of \(\epsilon\) and \(minPts\). Larger values of \(\epsilon\) will naturally lead to larger clusters as the \(\epsilon\)-neighborhood around each point grows. It makes sense then for \(\epsilon\) to remain small so as to avoid the formation of false positive clusters. Conversely, larger values of \(minPts\) will naturally lead to fewer clusters, albeit of larger size. The fact that the optimal \(\epsilon\) and \(minPts\) are both relatively small suggests that matching comparisons may not have many cells that “agree” on a registration, but the cells that do agree form a strong consensus (i.e., form tight clusters).
We also note the variability in the AUC values across the DBSCAN parameter space. Specifically, we see that the “\(C_0\) + Registration” models achieve the highest AUCs along a set of values in the bottom-left corner - where \(\epsilon \approx minPts\) for \(\epsilon,minPts < 10\). In our experimentation, we noticed that these \(\epsilon, minPts\) values are also where the cluster indicator \(C_0\) feature has highly-ranked importance (as is the case in ). Both the AUC values and the variable importance of \(C_0\) decrease as either \(\epsilon\) or \(minPts\) increase, which indicates that the \(C_0\) + Registration models rely heavily on \(C_0\) to distinguish between matching and non-matching comparisons. Comparatively, we see that the AUC values for the “All ACES” models are more consistently high across the parameter space, indicating a robustness to parameter choice.
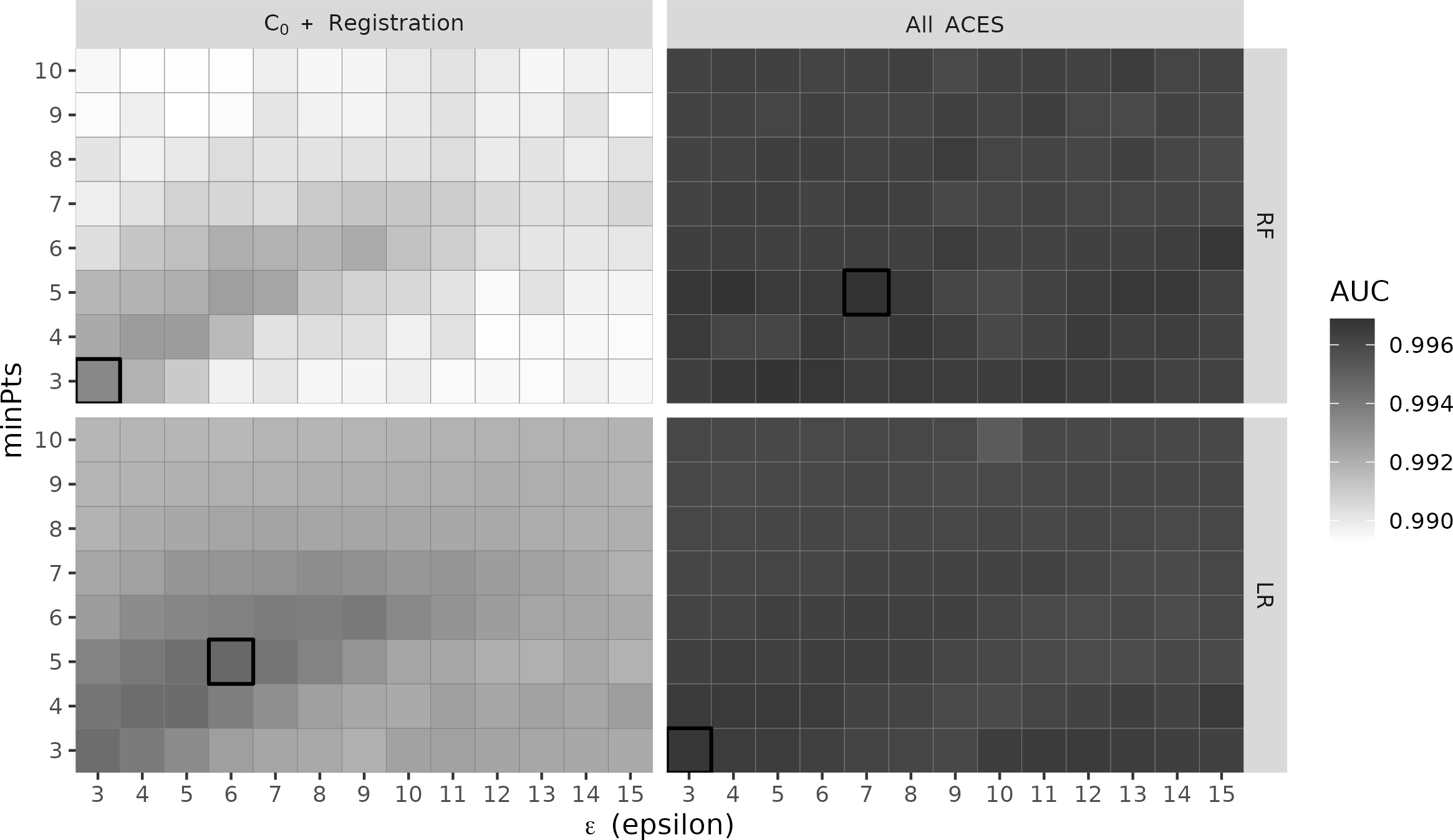
Figure 4.11: A heat map of AUC values associated with four classifier models across a grid of values for the two DBSCAN parameter \(\epsilon\) and \(minPts\). Darker tiles correspond with higher AUC. The four models are a combination of two feature groups (\(C_0\) + Registration vs. All ACES) and two models (Random Forest and Logistic Regression). The “All ACES”-trained models have higher and more consistent AUCs compared to the “\(C_0\) + Registration”-trained models.
To better understand the behavior of the AUC values in 4.11, consider 4.12 showing the Mean Gini Decrease for each of the 19 ACES features across the grid of \(\epsilon \in \{3,...,15\}\) and \(minPts \in \{3,...,10\}\) values. We see that the density Cluster Indicator \(C_0\), Cluster Size \(C\), and Translation Difference \(\Delta_{\text{trans}}\) have high variable importance for some combinations of \(\epsilon\) and \(minPts\), but are generally less consistent than the registration cell-based and full scan correlations \(\overline{cor}_{\text{cell}}\) and \(cor_{\text{full}}\). This implies that the density features can be highly informative under optimal conditions, yet quickly lose importance under sub-optimal conditions. In our experimentation, we noticed that other ACES features “take up the mantle” when \(C_0\) or \(C\) have low importance, which explains the relative stability in AUC values observed in the “All ACES”-trained models shown in 4.11.
The relationship between \(C_0\) and \(C\) (first two plots in the first row) is noteworthy by the sharp boundary defined by the line \(minPts = \epsilon\). Above this line, when \(minPts > \epsilon\), we see that \(C_0\) is considered more important than \(C\). In other words, as the minimum size required to be classified as a cluster (\(minPts\)) and the neighborhood radius (\(\epsilon\)) both become stricter, there will naturally be fewer clusters formed. In these instances, knowing whether a cluster is formed is more informative than the size of that cluster. However, the importance of \(C_0\) below the line, when \(minPts < \epsilon\), is seemingly replaced by \(C\) rising in importance. That is, when \(minPts\) and \(\epsilon\) are less strict, then more clusters will form and the actual size of the cluster becomes more informative than the fact that it exists.
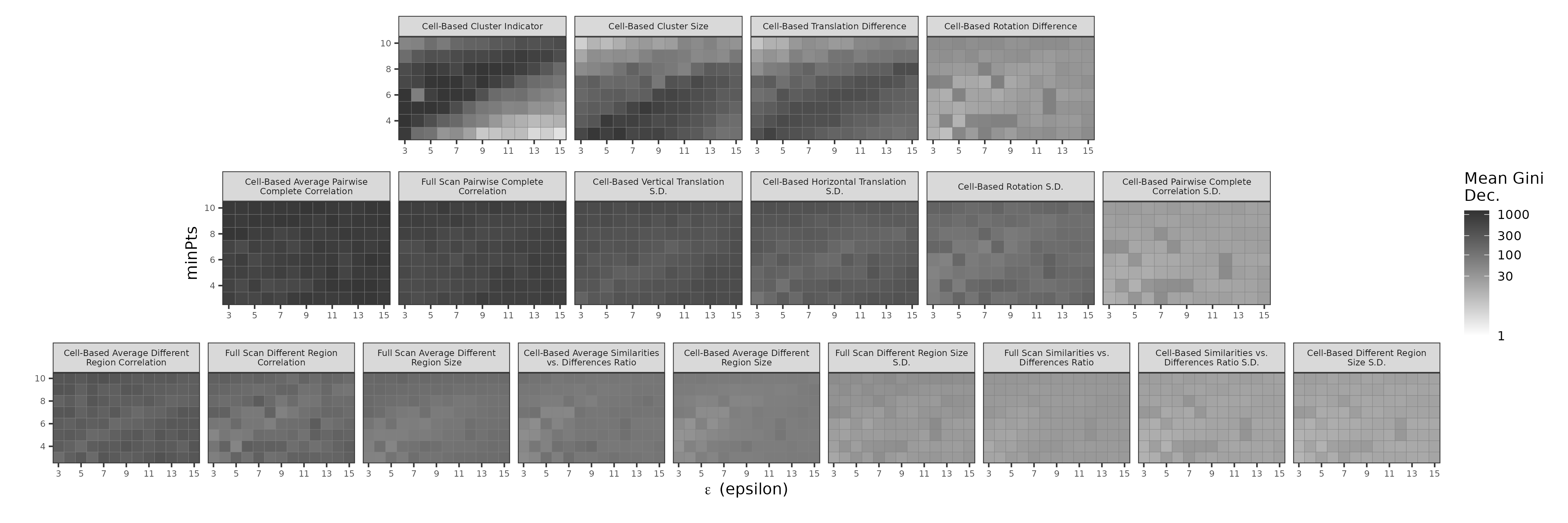
Figure 4.12: A heat map of variable importance measures for the 19 features in the ACES data set across a grid of values for the two DBSCAN parameter \(\epsilon\) and \(minPts\). Darker tiles correspond with higher importance. As in , we visualze the importance measures on a log-transformed color scale to more clearly see variability among smaller values. We see that features like the Cell-Based Cluster Indicator \(C_0\) and Cell-Based Cluster Size \(C\) have inconsistent importance measures across the difference values of \(\epsilon\) and \(minPts\) while the cell-based and full scan correlation features \(\overline{cor}_{\text{cell}}\) and \(cor_{\text{full}}\) have more consistent importance.
The \(\epsilon\) and \(minPts\) values are not the only parameters that can be tuned. We also computed the ACES features using two different cell grids: \(4 \times 4\) and \(8 \times 8\). Each cell in the \(4 \times 4\) grid captures a larger portion of the cartridge case’s surface compared to the \(8 \times 8\) grid, which would presumably be useful for the visual diagnostic-based features. However, the \(8 \times 8\) grid has the benefit of having more cells with which to measure consensus using the registration and density-based features. Our experimentation showed that the \(4 \times 4\) cell grid features resulted in categorically better classification results compared to the \(8 \times 8\) features. Throughout this paper, we present the \(4 \times 4\) results.
One would expect that having more cells would make it easier to measure the consensus. However, even the density-based features, such as the cluster size feature \(C\), had better separation between matching and non-matching comparisons when the \(4 \times 4\) cell grid was used compared to the \(8 \times 8\) grid. Further, performing classification using a combination of the \(4 \times 4\) and \(8 \times 8\) features actually led to lower overall test accuracy compared to just using the \(4 \times 4\) grid. We chalk this outcome up to the specific cell-based registration procedure we used. Recall from image registration algorithm that we first perform a pre-registration using the full scans and a rotation grid \(\pmb{\Theta}\). Using the full scan-estimated rotation \(\theta_d^*\), we then perform the cell-based comparison procedure using a limited rotation grid \(\pmb{\Theta}_d' = \{\theta_d^* - 2^\circ, \theta_d^* - 1^\circ,...,\theta_d^* + 2^\circ\}\).
To save on computational time, rather than comparing each source cell to the full target scan, we compare it to a slightly larger region that is located in the same position in the target scan (\(1.1 \times\) the side length of the source cell). Assuming the full scan registration was successful, a source cell isn’t allowed to “move” very far in this region to register. This in contrast to, for example, the original CMC methodology proposed in Song (2013) where each source cell is compared to a region in the target scan that is much larger, 2 or 3 times the side length. The consequence of our implementation is that cells, even for non-matching comparisons, tend to have registration values close to the origin (i.e., no movement), and are therefore more likely to form DBSCAN clusters compared to if we used larger target regions. In this case, a higher number of cells actually leads to a higher chance of forming “false positive” clusters for a non-match comparison, which is exactly what we observe from the \(8 \times 8\) comparisons. The formation of false positive clusters is far rarer in the \(4 \times 4\) cell grid case. We hypothesize that the \(8 \times 8\) cell grid results could improve if a different target region size were used. However, our implementation makes sense pragmatically, since the CCF computation grows exponentially with the size of the region cell or target region, and conceptually, since the full scan registration should result in a rough alignment of two matching scans before applying the cell-based comparison with a finer rotation grid.
4.5.3 Model Selection Considerations
Our intention in fitting the logistic regression and random forest classification models using different feature sets is to explore each model’s strengths and weaknesses. A critical step in putting the ACES algorithm into practice will be to settle on a single model. Pragmatically, it seems reasonable to choose the model with the highest estimated accuracy on available test data. However, we noted that models trained by this optimization criterion on imbalanced data tend to over-classify the majority class. This is the case for the CMC method results we summarized in Table 4.5, but is also true for ACES statistical models trained to maximize overall accuracy. For example, if we were to shift the similarity score classification threshold for the All ACES logistic regression model to maximize the overall accuracy on the training data, the resulting score threshold is 0.54 with test accuracy, true negative, and true positive rates of 99.4%, 99.9%, and 92.4%. Given the large true negative rate, we might favor this model from an ethical perspective since misclassifying a truly non-matching cartridge case pair may incriminate an innocent individual. However, the true positive rate is considerably lower than the “balanced” results summarized in 4.7. Further exploration of different optimization criteria is warranted.
Another aspect to consider when choosing a model is interpretability and explainability. If an algorithm is applied in forensic casework, then evidentiary conclusions derived from the algorithm’s output will inevitably be presented to a non-expert judge or jury. More interpretable models are easier to understand, and therefore should be preferred. The classification behavior of the logistic regression and classification tree models are arguably easier to explain than the random forest model. For example, the logistic regression model parameters can be understood in terms of the estimated increase in odds of a match. Paired with its comparable performance to the random forest, we propose the logistic regression model with all 19 ACES features as the preferred model that balances interpretability with accuracy.
4.6 Conclusion
In this paper, we introduced the Automatic Cartridge Evidence Scoring (ACES) algorithm to measure the similarity between two fired cartridge cases based on their breech face impressions. In particular, we defined a set of 19 similarity features and used these features to train and test classifier models. We validated our algorithm on a set of 510 cartridge cases - the largest validation study of a cartridge case similarity scoring algorithm to-date. Compared to predominant algorithms like the CMC algorithm described in Song (2013), the ACES logistic regression model achieves higher test accuracy rates while having more balanced true positive and true negative rates. We propose a logistic regression classifier trained on the ACES feature set as a new benchmark to which future scoring methods are compared.
Before the ACES algorithm can be put into practice, we must devise new stress-tests, using new ammunition and firearm combinations, to assess its robustness. There is also an opportunity to optimize additional parameters, such as the number of cells used in cell-based comparison or parameters used in pre-processing, to measure their effects on final results. A variety of factors, such as make/model and wear of the evidence or the algorithm parameters used, affect the discriminative power of the 19 features defined in this paper. We view the current version of the ACES algorithm as more a foundation for future improvements than a final solution. We expect the ACES feature set to evolve over time; for discriminatory features to replace less informative features. Given the gravity of the application, we stress interpretability as a guiding principle for future feature engineering and model selection. A misunderstood feature or result may lead a lay judge or juror to an incorrect conclusion. Additionally, we urge future researchers to use a train/test procedure similar to the one outlined in this paper to validate proposed methods.
We developed the scored R package as an open-source companion to this paper. The code and data used in this paper are available at https://github.com/jzemmels/jdssvSubmission.
References
If more than one cluster is identified, we binarize the points based on whether they were assigned to any cluster or if they are a noise point and proceed as if there is only one cluster. We assume that two or more clusters form only because of the course rotation grid considered. Were a finer grid used, the points would coalesce into a single cluster around the true translation value. This assumption has empirical support through our experimentation.↩︎